摘要: 本文的主要目的是要破除許多學生對於貝式定理「困難又不實用」的刻板印象。事實上,我們生活之中有許多情況必須要運用貝式定理的邏輯思考,否則便容易產生偏差甚至陷於謬誤。
對於許多上過統計課的學生而言,貝氏定理(Bayes Theorem)是又熟悉又陌生的。熟悉,是因為絕大多數的大學或研究所統計課堂都有教貝式定理;陌生,則是因為許多學生上完統計課之後,對於貝式定理仍然一知半解,甚至視為畏途。造成此現象的原因有二:首先,一般基本統計學教科書雖然會提到貝氏定理,但絕大多數的教科書仍然只涵蓋以P值檢定為基礎的傳統「次數統計推論」(frequentist statistical inference)。學生即使學了貝氏定理,也只把它當作一個數學公式,不知道它對學習統計學有什麼幫助,更不知道它具備生活實用性。其次,貝式定理的數學表示式難以背誦;即使一時背了,也容易忘記。以下是教科書上常見的貝式定理定義: 假定事件A和事件B發生的機率分別是 Pr(A) 和 Pr(B),則在事件B已經發生的前提之下,事件A發生的機率是
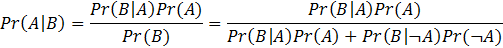
(其中「 」在邏輯上為「非」的符號:「 A」即「非A」)如果沒有充分理解機率運算的定義和法則,實在難以理解此公式背後的邏輯。許多學生因此強記上述公式以準備考試,只求能解題而不求理解;公式反而成為學習貝式定理的主要障礙。
本文的主要目的是要破除許多學生對於貝式定理「困難又不實用」的刻板印象。事實上,我們生活之中有許多情況必須要運用貝式定理的邏輯思考,否則便容易產生偏差甚至陷於謬誤。
舉例來說,每逢有人因車禍不幸橫死,當記者報導死者是孝子,我們常唏噓說為何橫死的都是好人?這樣的想法,其實犯了諾貝爾經濟學獎得主、心理學家 Daniel Kahneman 所說的「基率謬誤」(base rate fallacy)。簡單來說, 就是沒有把「絕大多數人都是好人」這個「基率」—貝氏定理所謂的先驗機率(prior probability)—納入考量所致。因為絕大多數人都是好人,即使老天爺真的大致上賞善罰惡,橫死的人也會大多是好人,更不用說車禍應該跟善惡無關了。比如我們假設每100人中只有1人(1%)是十惡不赦的「壞人」,其餘99人(99%)都是「好人」。再假設90%的壞人果然都遭車禍橫死,而只有10%的好人意外橫死。這樣老天算是有眼了,可是如果今天有人意外橫死,請問他是好人的機率多少呢?用貝氏定理可以算出Pr(好人|橫死)=0.92,也就是橫死的人中有92%會是「好人」,只有8%是壞人!這正是因為大部分人都是好人,出事的當然容易是好人,即使老天有眼也是一樣。
貝氏定理的原理就是在先驗機率的基礎上,納入新事件的資訊來更新先驗機率,這樣算出來的機率便叫做後驗機率(posterior probability)。以前述好人橫死的例子來說,先驗機率的分配是 Pr(好人)=0.99及Pr(壞人)=0.01。在無其他資訊的情況下,我們在街上隨機遇到一個人,此人為好人的機率是0.99。但現在此人被車子撞死了,根據我們對老天有眼的假設(Pr(橫死|好人)=0.1及Pr(橫死|壞人)=0.9),好人不容易橫死,而此人橫死了,這新事件的資訊可以讓我們用貝氏定理來計算後驗機率Pr(好人|橫死)=0.92,也就是此人為好人的機率變小。這就是所謂「貝氏更新」(Bayesian updating):新事件的資訊改變了我們原來的估計。如果我們沒有把先驗機率納入計算,我們很可能因為相信老天有眼,橫死的應該大多是壞人,就斷此人很可能是壞人。而若確定此人是好人,我們就唏噓不已,甚至怨罵老天。這兩種反應的人其實都犯了「基率謬誤」。當然,如果車禍跟人的好壞無關,也就是不論好人壞人橫死的機率都一樣,則有人橫死的新事件是不會更新我們對他是好人或壞人的基率的。
Kahneman在《快思慢想》一書中舉了一個也是跟車禍有關的「基率謬誤」的例子。某天夜晚城裡發生了一件車禍,肇事的車子逃逸,但有證人指認那是一輛藍色的計程車。城裡只有藍色、綠色兩種計程車;綠色車佔85%,藍色車僅佔15%。法庭檢驗證人在夜晚識別車色的能力,發現他識別正確的機率是80%,而識別錯誤的機率是20%。當Kahneman做實驗問受測者肇事車輛為藍色的機率多少時,大部分人的答案是80%。這也是犯了「基率謬誤」的答案,也就是城裡「綠色車佔85%,藍色車佔15%」這個基率所包含的資訊被忽略了。如果把基率納入考量,貝氏定理給的答案是Pr(肇事車真為藍色|證人指認為藍色)=0.41,只有一般人想像中的一半!
現實生活中類似的例子很多:身體檢查某項檢驗得到陽性反應、職棒大聯盟球員沒通過藥檢、犯罪現場採得的DNA與調查局資料庫CODIS中某人的DNA相符、甚至統計上P值檢定得到顯著結果。這些情況中,如果我們不了解貝氏定理,我們很可能就會在機率估計上犯錯。那麼貝氏定理究竟要如何拿來計算正確的後驗機率呢?本文將用淺易的途徑來介紹貝氏定理的計算方法。 聯合機率(joint probability)、邊際機率(marginal probability)以及條件機率(conditional probability)
欲瞭解貝式定理的邏輯,必須先瞭解三種不同的機率:聯合機率、邊際機率以及條件機率。假設有兩個隨機變數(random variable)X和Y,變數X有1, 2, ..., J共J個可能的值,而變數Y有1, 2, …, I共I個值。在此可以將變數的「值」視為前面提及的「事件」(event),舉例來說,X代表大聯盟球員有沒有使用禁藥,X=1代表「沒有使用」,X=2代表「有使用」;Y代表藥檢的結果,Y=1代表「陽性反應」,Y=2代表「陰性反應」。這裡X=1、X=2、Y=1、Y=2都是其發生有一定機率的事件。如果我們想要檢視X和Y之間的關係,可以繪製出下列交叉表:
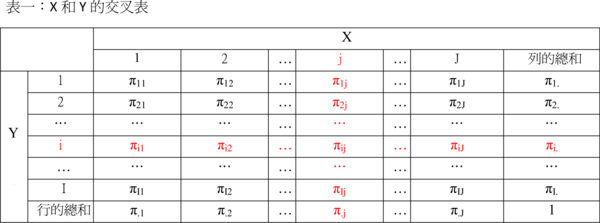
我們先從概念開始介紹。表一所陳列的Y跟X聯合起來所有可能的結果可以用 {(1,1), (1,2), …, (i,j), …, (I,J)} 這個集合來表示,這就是Y跟X聯合起來的「樣本空間」,它一共有IxJ個可能結果。每一個結果所對應的機率是Y跟X的聯合機率,也就是屬於Y的事件Y=i和屬於X的事件X=j聯合發生的機率,數學表示為Pr(Y=i,X=j)=πij。例如π11就是Y=1和X=1這兩個事件都發生的機率,π12則是Y=1和X=2這兩個事件都發生的機率,以此類推。如果我們把所有可能結果的機率加總,從π11加到πIJ,總和必須是1。 邊際機率則是屬於Y或X的單一事件發生的機率。表一中,Y的樣本空間是 {1, 2, …, i, …, I};屬於Y的事件發生的邊際機率用Pr(Y=i)=πi.表示。X的樣本空間是 {1, 2, …, j, …, J};屬於X的事件發生的邊際機率用Pr(X=j)=π.j表示。例如π1.就是Y=1這個事件發生的機率,π.2則是X=2這個事件發生的機率,以此類推。Y或X所有邊際機率的總和也必須是1。在表一裡,我們以行或列的總和來計算邊際機率。邊際機率其實就是單一變數的機率分配,之所以稱為邊際機率指是因為我們從表一的雙變數聯合機率分配的脈絡出發,導出單一變數分配的緣故。
最後,條件機率是在屬於X的事件已經發生的前提之下,屬於Y的事件發生的機率,或是在屬於Y的事件已經發生的前提之下,屬於X的事件發生的機率。例如Pr(Y=i|X=j)是在X=j這個事件已經發生的前提下,Y=i這個事件發生的機率;而Pr(X=j|Y=i)是在Y=i這個事件已經發生的前提下,X=j這個事件發生的機率。
條件機率的樣本空間只是聯合機率樣本空間的一部份。在表一中,Y跟X聯合起來的樣本空間一共有IxJ個可能結果。但當我們以X=j這個事件已經發生為前提時,Y這個變數的樣本空間就被侷限在 {(1,j), (2,j), …, (i,j), …, (I,j)} 這I個結果的範圍裡。同樣的,當我們以Y= i這個事件已經發生為前提時,X這個變數的樣本空間就被侷限在 {(i,1), (i,2), …, (i,j), … (i,J)} 這J個結果的範圍裡。因為樣本空間改變,機率也會有所不同。其計算如下:
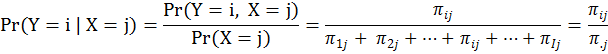
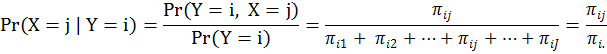
這也就是說:條件機率等於聯合機率除以條件變數的邊際機率。反過來講:聯合機率等於條件機率乘以條件變數的邊際機率,如下式所示:
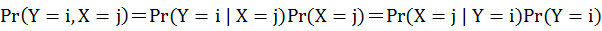
此公式稱為機率的乘法法則(Multiplication Rule),這個法則對於理解貝式定理至關重要。
前述提及條件機率有兩種,分別為Pr(Y=i|X=j)以及Pr(X=j|Y=i),差別僅在於是以X變數的特定事件為給定前提,還是以Y變數的特定事件為給定前提。表一中,因為X是「行」(column,台灣稱「行」,中國大陸稱「列」)的變數,我們把以X變數特定事件為給定前提的條件機率稱之為「行的條件機率」(column conditional probability);如果是以Y變數特定事件為給定前提的條件機率,因為Y是「列」(row,台灣稱「列」,中國大陸稱「行」)的變數,我們稱之為「列的條件機率」(row conditional probability)。
Pr(Y=i|X=j)以及Pr(X=j|Y=i)這兩個機率,我們可以說它們互為「反機率」(inverse probability)。我們以X和Y分別只有兩個值為例,以表二和表三加以說明:
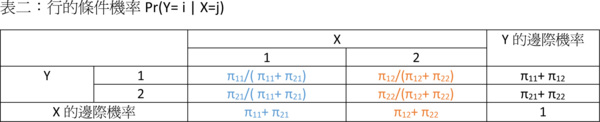
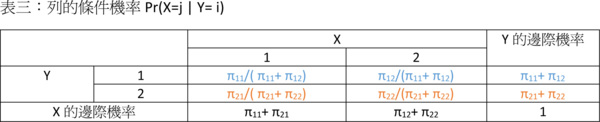
接下來要進入本文的主題了,究竟貝式定理是什麼,怎麼算?說穿了,貝式定理就是將行的條件機率轉變成列的條件機率,或是將列的條件機率轉變成行的條件機率。貝式定理公式看似複雜,背後邏輯其實相當簡單,它就是一個將「給定X事件已發生的前提下,Y事件發生的條件機率」轉變成「給定Y事件已發生的前提下,X事件發生的條件機率」的過程而已。換句話說,貝氏定理就是在算反機率。
我們先用一個簡單但實用的例子來說明這個觀念。這個例子出自「看電影學統計: p值的陷阱」一文:美國職棒大聯盟(Major League Baseball)抽查球員是否使用禁藥PED(performance enhancing drugs),結果某明星球員藥檢測出有陽性反應。我們要問的是:這位明星球員其實是清白的機率是多少? 要算這個機率, 我們必須要有球員是否使用PED的先驗機率,也就是在還未對球員實施藥檢之前,我們必須先對他是否使用PED的機率有一個初步估計。這個估計可能相當主觀,但也未嘗不能用客觀的數據加以估計,比如之前抽檢的結果。另外,我們還必須知道藥檢的準確率,也就是球員真有使用PED時藥檢結果呈現陽性的機率,和球員沒有使用PED時藥檢結果呈現陰性的機率。 假設我們擁有的這兩項資訊如下:
• 根據以前的藥檢結果,我們合理估計大約有6%大聯盟球員有使用PED。
• 藥檢的準確率為0.95:如果球員真的使用了PED,藥檢結果呈現陽性的機率是0.95;而如果球員沒有使用PED,藥檢結果呈現陰性的機率也是0.95。(這兩個機率不必一樣。)
第一項資訊提供了貝氏定理所需要的先驗機率,也就是在明星球員還沒實施藥檢前,我們對他是否使用PED最好的猜測只能是0.06的機率有使用,0.94的機率沒使用。第二項資訊告訴我們大聯盟的藥檢的「偽陽性」(false positive)機率—球員並未使用PED但藥檢結果呈陽性反應的機率—是0.05,「偽陰性」(false negative)機率—球員有使用PED但藥檢結果呈陰性反應的機率—也是0.05。
如果我們的明星球員藥檢呈陽性反應,我們可能會認為藥檢結果錯誤的機率只有0.05。但這是沒有考慮先驗機率的想法,我們這樣想就是犯了「基率謬誤」。要考量先驗機率,必須要使用貝氏定理來算後驗機率,也就是要算出「偽陽性的反機率」。
我們用Y來代表「藥檢結果是陽性還是陰性」的隨機變數;Y=1代表藥檢結果呈陽性反應,Y=2代表藥檢結果呈陰性反應。我們再用X來代表「球員有沒有使用PED」的隨機變數;X=1代表沒有使用,X=2代表有使用。這樣定義之後,我們可以看出:先驗機率是X的邊際機率Pr(X=1)=0.94,Pr(X=2)=0.06。藥檢的準確率和偽陽性、偽陰性機率都是行的條件機率:Pr(Y=1|X=1)=0.05,Pr(Y=2|X=1)=0.95,Pr(Y=1|X=2)=0.95,Pr(Y=2|X=2)=0.05。我們將這些數據放到表二之中可以得到下列表四:
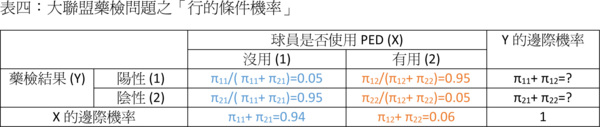
前面說過貝式定理就是將行的條件機率轉變成列的條件機率,或是將列的條件機率轉變成行的條件機率。現在我們已經有行的條件機率了,那麼怎麼求列的條件機率呢?首先我們必須先要算出Y跟X的聯合機率和Y的邊際機率。算聯合機率必須使用機率的乘法法則
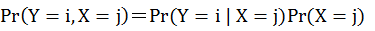
也就是把行的條件機率跟X的邊際機率相乘。就是在這裡,我們必須要用到X的先驗機率!聯合機率算出來之後,把各列的聯合機率加總就得到Y的邊際機率:
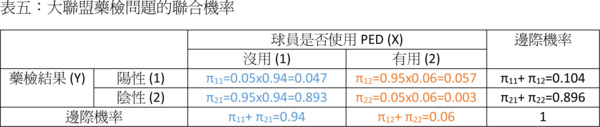
有了聯合機率跟Y的邊際機率,我們就可以輕易計算列的條件機率了:
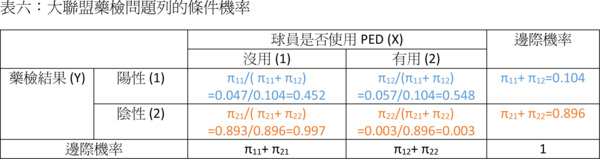
事實上,如果我們只是要算「藥檢結果是陽性而實際上球員是清白的機率」,我們只要算左上角 Pr(X=1|Y=1) 這個機率就夠了:
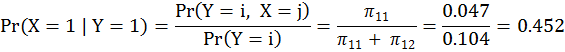
以下我們提供第二個例子:用貝氏定理來求解有名的「蒙提霍爾」電視遊戲問題。 蒙提霍爾問題(Monty Hall Problem)
這是美國電視台一個相當有名的電視遊戲,相信不少讀者都已聽過,我們在此簡單介紹一下。這個遊戲一開始,主持人(Monty Hall)給妳看三道門。他告訴妳:三道門中,有一道門後面有一輛汽車,另外兩道門後面各有一隻山羊。Monty要妳挑選一道門,但先不要打開。妳挑定了一道門之後,Monty打開另外兩道門之一,顯示門後有一隻山羊。這時Monty問妳要維持本來選定的門,還是要換選那一道沒開的門。如果妳選到藏有汽車的那道門,便可贏得汽車,否則便贏到山羊。。
這個遊戲的答案是要換,理由很簡單,並不需要用貝氏定理來算。參賽者原來隨機選擇的門可以猜中汽車的機率是1/3,那麼汽車在另兩個門其中之一後面的機率就是2/3。現在Monty開了兩個門其中之一,其後並無汽車,那麼這2/3的機率便完全屬於另一道門了:參賽者如果換門,抽中汽車的機率將加倍!雖然如此,當號稱全世界IQ最高的專欄作家Marilyn vos Savant這樣解釋時,很多讀者不相信。包括數學教授在內的眾多讀者都批評她,說她錯了。這些讀者認為還未開的兩道門可以猜中汽車的機率應該一樣,換門並沒有用。 因為這個問題相當有趣,而且比上例要複雜些,這裡我們用它來幫助我們學習貝氏定理。在此例子之中有兩個變數:汽車的位置和主持人開啟的門,兩個變數各自有三種可能結果:1號、2號以及3號門,交叉相乘可以有九種可能的事件組合。
我們假設參賽者一開始猜選的們為1號門(在下表中用【1】表示),接著主持人要開啟2號或3號門之中後面藏有山羊的那一道門。此時我們必須要知道:第一,按照規則,在參賽者選了1號門之後,主持人就不能開啟1號門,不論1號門後面是山羊或汽車都是如此;第二,哪一號門會被主持人開啟?這事件的機率皆為條件機率,因為主持人是在已知汽車是在哪一道門後面的前提下做出的選擇;第三,主持人理所當然不會開啟後面有汽車的那道門。我們以M代表主持人做出的選擇。
如果汽車就在1號門後面,那2號和3號門後面皆為山羊,因此在參賽者猜了1號門的情況下,主持人可從2號及3號門之中隨機選一道門開啟,因此Pr(M=2|C=1)與Pr(M=3|C=1)條件機率皆為1/2。如果汽車在2號門後面而參賽者猜了1號門,主持人在不能開啟1號門和2號門的情況下只能開啟3號門,因此Pr(M=3|C=2)=1,此規則也適用在汽車在3號門後面的情況。當然,參賽者只能看到主持人開了什麼門,根本不知道主持人葫蘆裡賣什麼藥。 據此,我們可以填出表七的先驗機率及條件機率並以之求得表八的聯合機率:
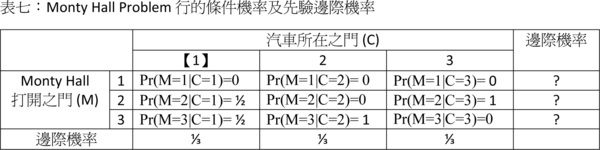
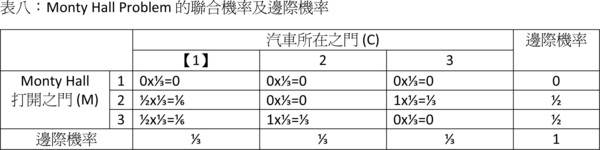
接下來就是直接求列的條件機率了:
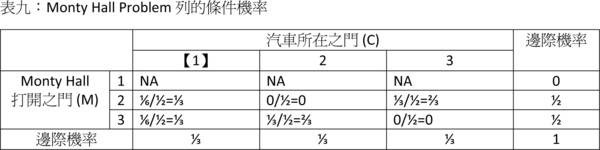
這個表第二列的詮釋如下:假設主持人開啟了2號門,則門後是汽車的機率為0(按照規則),而參賽者維持1號門和改變主意改選3號門這兩種策略抽中汽車的機率分別是1/3和2/3。這兩個機率是「在已知主持人開啟2號門的給定前提之下,汽車在1號或3號門後面」的列的條件機率,在已知所有聯合機率的情況下,我們可以用條件機率的定義輕易算得:
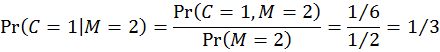
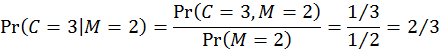
這就是為何參賽者更改選擇至3號門抽中汽車的機率(2/3)會比維持原初1號門猜測而抽中汽車的機率(1/3)還要高的由來。有興趣的讀者不妨試算「在主持人開啟3號門的前提下」的條件機率,會發現結果仍是一致的:更換選擇抽中汽車的機率仍是2/3,不更換抽中汽車的機率仍是1/3。 正是因為一開始參賽者猜對的機率是1/3、猜錯的機率是2/3,致使主持人開啟一道後面是山羊的門的時候,如果參賽者換選僅剩的那道門會有2/3的機率猜對。貝式定理以數學方式釐清了這一點。
貝式定理在統計學的應用越見廣泛,也讓許多學生以為貝式定理只有跟「貝式統計推論」(Bayesian statistical inference)相關,沒用到貝式統計分析就不需要學會。其實貝式定理在生活之中是很有用的,本文以淺顯的方式介紹貝式定理的邏輯和計算方法,不僅期望讀者在學貝氏定理時確實理解那些複雜公式的由來,也希望讀者將貝式定理的邏輯思維運用到日常生活之中。要學會貝氏定理才能避免「機率謬誤」,正確地用新事件的資訊來更新我們原所信仰的先驗機率。
轉貼自: 林澤民的部落格
若喜歡本文,請關注我們的臉書 Please Like our Facebook Page: Big Data In Finance


留下你的回應
以訪客張貼回應